A végtelen
Szó-lélek-közelítés 21.
„Az Isten mélységét elérheted-é, avagy a Mindenhatónak tökéletességére eljuthatsz-é?” (Jób 11:7)
A „végtelen” kifejezés hétköznapi használata sokszor nincs összhangban a mélyebb jelentésével. A végtelen szó határtalan, vég nélküli megszámlálhatatlanságot jelöl, s az ember tudatra ébredése óta töpreng ezen, noha a kizárólag véges természetű tapasztalataink alapján próbáljuk egyáltalán a fogalmat kialakítani. Megközelíteni csak gondolkodás útján lehet, közvetlen szemlélettel meg nem fogható, pedig a csillagos égre tekintve valamennyien szeretnénk megfejteni. Leopardi írta:
„Gondolatom a határtalanba merül; s ebben a tengerben oly édes megsemmisülni.”
A teológiában Isten végtelen természete képességeinek határtalanságára utal, nem mennyiségbeli végtelenségre. Véges elme nem képes teljesen felfogni a Végtelen jellemvonásait és munkáit. Istennek a velünk való bánásmódját csak annyira tudjuk megérteni, amennyire fölismerjük határtalan kegyelmének egyesülését végtelen hatalmával. Balassi végtelen irgalmúnak nevezi, a hitvalló énekek is elcsodálkoznak:
„Kezdete sohasem volt a te idődnek, esztendei soha el nem végeződnek… Láthatatlan lélek, te betöltesz mindent, jelen vagy itt alant, valamint odafent” (247. ref. ének);
„Az egek boltjai alatt forgó világok mély bölcsességéről beszélő bizonyságok. Ki ruházott fényt a sok ezer napokra? Ki indítá útnak a számtalan földeket?” (248. ref. ének).
Az antik tudósok nem egy-egy tudományterület szakértői voltak, hanem elsősorban filozófusok, gondolkodók. Így több irányból is eljuthattak a korlátlan végtelen fogalmához: a fizikából, a csillagászatból vagy a matematikából. Eukleidész Elemek című összefoglaló művében belátja, hogy „prímszámból prímszámok bármely adott sokaságánál több van”, vagyis végtelen sok prímszám van, bár ezt nem mondja ki. A hindu matematikában először Ácsárja Bhászkara írásában jelenik meg a végtelen, pl. a nullával való osztás problémájánál. A matematika a végtelen fogalmának szigorú kezelésére több megoldást használ. Arisztotelész elismerte, hogy „sok képtelenség következik a végtelen tagadásából is és a végtelen elismeréséből is”. Kétfajta végtelent különböztetett meg: az aktuális, meglévőt és potenciális, keletkezőt. A potenciális végtelen a dolgok vagy jelenségek olyan sorozata, amit minden határon túl lehet folytatni, vagyis mindig lehet nagyobb természetes számot mondani. Ezzel szemben aktuális végtelen például a természetes számok összessége, egy végtelen halmaz. A matematikai halmazelmélet a végtelennek többféle fogalmát különbözteti meg, amelyeket nagyság szerinti sorba tud állítani. A legkisebb a megszámlálható végtelen, aminek meg tudjuk számolni az elemeit, azaz minden eleméhez tudunk mondani egy pozitív egész számot, úgy, hogy minden számot csak egyszer használunk föl. Nem tudjuk azonban megszámolni a valós számokat, az egészekből álló sorozatokat, vagy a valós számokat valós számokba képző függvényeket. Egyes matematikai elméletekben a valós számokat kiegészítették végtelen elemekkel, és az így kapott halmazon újraértelmezték a műveleteket. A modern matematikai analízis lépett jóval tovább, a differenciál- és integrálszámítással.
A differenciál- és integrálszámítás elemei
A határérték megjelenése pedig a végtelen közelítés módszerének fogalommá alakítása.
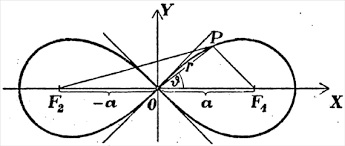
A geometriában sokszor szemléletes egy végtelen távoli pontot elképzelni, például a parabolát egy ellipszisnek tekinteni, amelynek egyik fókuszpontja végtelen távol van. Ezen ideális pontok szigorú kezelése adja a projektív geometriát.
A filozófiában többször alkalmazzák a végtelen fogalmát a térre vagy az időre vonatkoztatva, például Kant az első antinómiájában, illetve foglalkoznak a végső, az abszolút fogalmával és Zénón paradoxonjaival. Ezek közül egyik az „Akhilleusz és a teknős”. Zénón a tér és idő korlátlan oszthatóságából kiindulva fogalmazza meg ezt a feladványt. Akhilleusz, a leggyorsabb görög, versenyt fut a nála lényegesen lassabb teknőssel, annak 100 láb előnyt adva. Akhilleusz pár pillanat alatt ott terem, ahonnan a teknős indult, azonban eddigre a teknős is haladt valamennyit. Akhilleusz egy újabb lépéssel ott van, ám ezalatt a teknős ismét halad egy kicsit, és még mindig 
vezet. Akármilyen gyorsan is ér Akhilleusz oda, ahol a teknős egy pillanattal korábban volt, amaz mindig egy kicsit előrébb lesz. Így a fogalom jelentése a Kiss Gábor szerkesztette Régi szavak szótárában (Tinta Könyvkiadó, 2012, 2018) szereplő végetlennel azonos. A XIX. században az analízis eszközeivel közelítették a kérdést. A futás tetszőleges szakaszát tekintve, a megtett utak és az ehhez szükséges idők összege is véges. Tehát sem távolságban, sem időben sincs szó végtelenségről, s ezzel a meggondolással föl is oldották a paradoxont. Anaximandrosz, ókori görög filozófus először mondta ki a sejtést a világmindenség végtelenségéről, így próbálta megvilágítani a korlátlan fogalmát: „Bárhol is áll a katona, lándzsáját ki tudja nyújtani még valamivel messzebbre.”
A végtelen gondolata szorosan összekapcsolódik az örökkévalósággal mint az idő végtelenségével. A sokféle láttató erejű kép közül az egyik, ókori keletről származó példázat így szól: Egy gyémánt hegy csúcsára százévente egyszer leszáll egy madárka, s megköszörüli rajta a csőrét. Ha az a hegy teljesen elkopik, ekkor telik le egy pillanat az örökkévalóságból. De nem kell az ókorig visszanyúlni, hogy ilyen példát találhassunk, hazánk népdalkincsében is előfordul hasonló kép:
„Látod-e babám, látod-e babám, amott azt a nagy hegyet?
Még azt látod, még azt látod, én a tied nem leszek.
Azt a hegyet a zsebkendőmnek a négy sarkában is elhordom,
Mégis az enyém, mégis az enyém leszel, édes galambom.”
József Attila pedig lírába oldja:
„Végtelen óta folynak a percek,
Végtelen óta folynak a könnyek –
Harsog a tenger, árad a tenger
És jaj! utánok még többen jönnek.”
Általánosan használt jele a vízszintes, fekvő nyolcas, a lemniszkáta a végtelenség és a korlátok nélküliség szimbóluma is, a soha meg nem szűnő áramlás jelképe, és ezzel a reinkarnációé, az újra megtestesülésé. Az élet ősi ritmusára szintén utal, valamint a befejezettség, az utolsó ítélet száma is. Carl Jung pszichológus és pszichiáter a nyolcast a tudattalan sötét és titkos mozgásával azonosította, Ady pedig így sóhajtott:
„Vágy, emlék, bánat, cél, okság,
Egy pillanatnyi jóllakottság”.
A szimbólum szerkezetét tekintve az egységet, a szférák közti egyenlőséget és azok egymásba olvadását is jelképezi. A keleti kultúrákban, Kínában és Tibetben ez a jelkép a végtelen csomó, mely az élet kifürkészhetetlen mivoltát jeleníti meg. Egymásba fonódó vonalai a világ ok-okozati összefüggéseire utalnak. Itt említhetjük a rokon értelmű szóként Kiss Gábor és Bárdosi Vilmos Szinonimák 
című kötetének (Tinta Könyvkiadó 2008, 2012) példáját: beláthatatlan. A vonal kezdet és vég nélküli megjelenítése Buddha végtelen bölcsességét, valamint a természet és az emberi élet örök körforgását szimbolizálja. A kölcsönös függést is jelenti, az univerzumban minden mindennel összefügg. Az ösvényen haladás ideje alatt a bölcsesség és a módszer egyesülését, az üresség és függő keletkezés elválaszthatatlanságát, és végül a megvilágosodást elérve a bölcsesség és a könyörületesség teljes egyesülését jelképezi. A japán és a kelta kultúrában is megvan az örökkévalóság jeleként az önmagán többször átbújó hurok. A magyar népművészetben a ruhák sujtása tartalmazza a végtelen csomó motívumát.
Díszmagyar huszár dolmány
Fekete István Végtelen verse a korláttalan lét sugalmát érezteti:
Hűvös, színtelen pára:
a föld s a fák lélegzete, felhők fia, ősz uszálya,
halott hajnalok holt keze.
Majdnem nincs. Semmi… mégis
mindenütt ott van, fenn és lenn,
szájban és szívben, szóban és hitben,
és ha van: nincs, s ha nincs: Minden.
Sümeginé dr. Tóth Piroska
A Szó-lélek-közelítés sorozatban korábban megjelent:
